IPO季报|国泰海通撤单数量最多 国新证券协助“带病闯关”失败储备项目归0
- 生活百科
- 2025-04-03 19:27:04
- 7
- 更新:2025-04-03 19:27:04
登录新浪财经APP 搜索【信披】查看更多考评等级
炒股就看金麒麟分析师研报,权威,专业,及时,全面,助您挖掘潜力主题机会!
出品:新浪财经上市公司研究院
作者:IPO再融资组/郑权
在刚刚过去的3月份,A股合计有8家企业IPO申请获受理,今年一季度合计受理9家。3月份上会4家企业,全部过会;今年一季度共有8家企业上会接受审核,全部过会。
3月份,A股共有10家企业终止IPO进程。今年一季度,A股共有52家企业终止IPO,其中主动撤回46家,终止注册6家。保荐券商中,国泰君安+海通证券撤回的数量最多,为6.5家。多家券商撤回IPO项目后储备项目归零。
发行及募资层面,3月份合计有14家企业上市,较2月份的1家环比大幅增长;3月份14家IPO企业合计募资92.18亿元,环比增长7195%。今年一季度,A股共有27家企业IPO,合计募资164.76亿元,较2024年第一季度同比下降30.24%。
IPO终止情况:海通证券协助赛克赛斯“带病闯关”失败 多家中小券商储备项目归0
今年3月份,A股共有10家IPO企业终止。今年1-3月份,A股合计52家企业终止IPO,其中创业板、北交所、上证主板、深证主板、科创板分别有18家、16家、10家、6家、2家企业终止。
分券商看,中信证券、中信建投、海通证券一季度分别有5家、4家、3.5家企业IPO终止,位列前三。东方证券、国泰君安、国金证券、国信证券、民生证券分别有3家企业终止。如果将国泰君安和海通证券的数量相加,国泰海通一季度IPO终止项目数量最高。
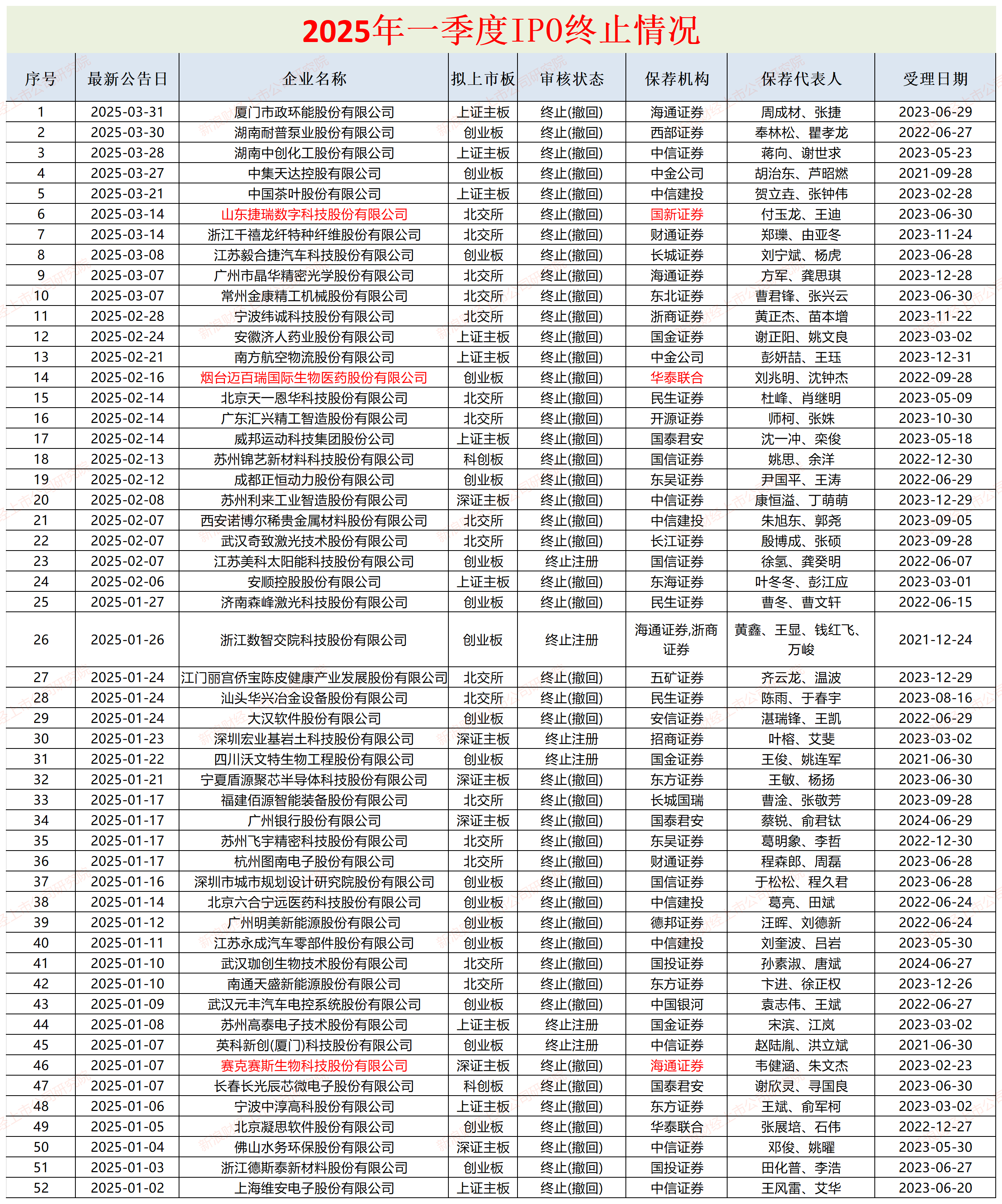
海通证券撤回的3.5家企业分别是厦门市政环能股份有限公司、广州市晶华精密光学股份有限公司、浙江数智交院科技股份有限公司(与浙商证券联合保荐)、赛克赛斯生物科技股份有限公司(下称“赛克赛斯”)。
其中,赛克赛斯主营业务是植介入生物材料类医疗器械的研发、生产和销售。2020年,赛克赛斯申报科创板IPO,经历了两轮问询后撤回申请。2023年,赛克赛斯转道深交所,审核期间被抽中现场检查。
现场检查发现,赛克赛斯业务推广相关内部控制存在薄弱环节,包括未对CSO服务商是否符合规定的准入条件进行实质审查、对CSO服务商推广活动监督抽检比例较低等,相关审核问询回复与实际情况不符,未能保证发行上市申请文件和信息披露的真实、准确、完整。
海通证券作为赛克赛斯的保荐券商,因未充分关注并审慎核查发行人业务推广相关内部控制薄弱环节及部分推广活动验收存在瑕疵、资金流水核查取证不充分、对终端客户走访、视频访谈程序不到位等问题被采取书面警示。
随着大量IPO项目终止,部分中小券商的撤否达到100%,并且储备项目归零,如五矿证券、国新证券、长城证券、长城国瑞、东海证券等。
其中,国新证券的保荐独苗山东捷瑞数字科技股份有限公司(捷瑞数字),2022年的扣非归母净利润仅2617.37 万元,刚刚满足北交所上市标准。捷瑞数字实控人之一为孙伟杰,孙旗下有杰瑞股份和德石股份两家上市公司。北交所在问询函中多次提到“是否通过关联交易、特殊安排等满足上市标准”。
据北交所官网信息,捷瑞数字及高管因信披违规被北交所出具警示函,国新证券及相关人员也收到警示函,但未公开详细信息。
还是根据捷瑞数字问询函内容,国新证券的保荐质量确实较差,包括“关联交易的必要性、公允性论证不充分”、存在漏答等问题。北交所甚至要求国新证券质控、 内核部门就项目执行过程中是否严格遵守依法制定的业务规则和行业自律规范的要求,是否严格执行内部控制制度,是否能有效保证执业质量等进行说明。
除了海通证券、国新证券两家券商保荐的IPO项目外,华泰联合因为协助保荐项目“带病闯关”遭罚。
华泰联合保荐的烟台迈百瑞国际生物医药股份有限公司(迈百瑞),是一家专注于生物药领域的CDMO企业,在最初版本的申报材料中,迈百瑞将2019年度费用“-19306万元”错误披露为“19306万元”,导致扣非净利润从-6545.75万元错误披露为-45157.75万元,差异高达3.86亿元。华泰联合对这个低级错误丝毫没有察觉,因此收到了书面警示。
IPO发行情况:恒鑫生活承销保荐费用率偏高 华安证券“一口吃个胖子”?
wind显示,3月份合计有14家企业上市,较2月份的1家环比大幅增长;3月份14家IPO企业合计募资92.18亿元,环比增长7195%。今年一季度,A股共有27家企业IPO,合计募资164.76亿元,较2024年第一季度同比分别下降30.24%。
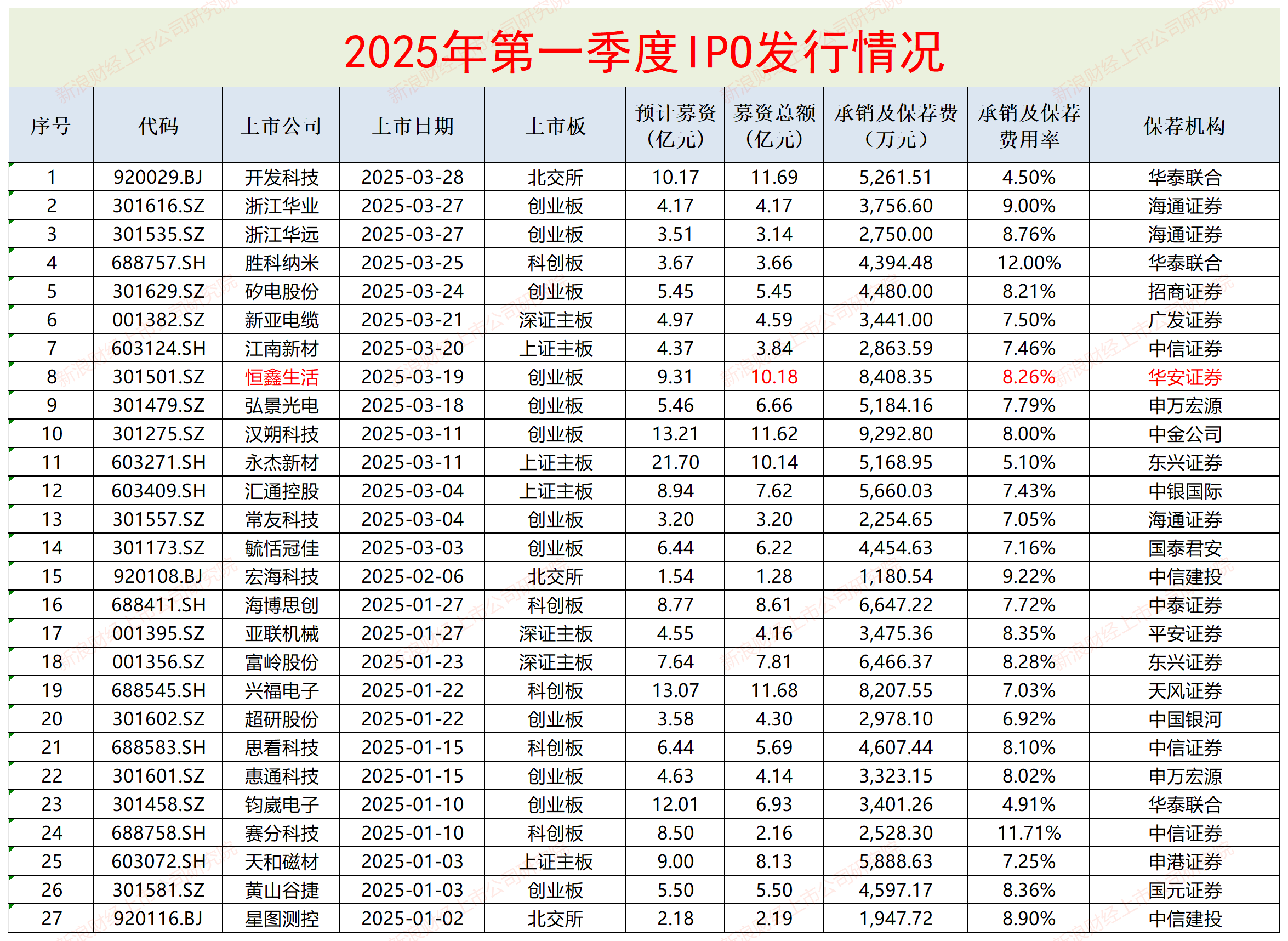
27家新上市的企业中,开发科技今年一季度的募资额最高为11.69亿元,该募资额是北交所2021年以来最高的募资额;募资额最低的也是来自北交所的宏海科技,实际募资1.28亿元。
27家企业中,仅10家公司实际募资符合预期,17家不及预期,占比63%。其中赛分科技预计募资8.5亿元,实际募资2.16亿元,实际募资比例仅不及预期的四分之一,中信证券保荐承销。此外,永杰新材计划募资21.7亿元,实际募资10.14亿元,较预期缩水53%,东兴证券保荐承销。
一季度上市的27家公司中,只有2家公司的发行市盈率超过行业市盈率均值,这两家公司分别是赛分科技、胜科纳米,发行市盈率分别是行业市盈率均值的1.71倍、1.17倍。有意思的是,赛分科技在高发行市盈率之下,实际募资额仍严重不及预期。
发行费用率方面,依然是赛分科技最高为23.2%,是27家公司中唯一一家超过20%的企业;开发科技发行费用率最低,仅为5.14%。
27家公司中,承销保荐费用最高的是汉朔科技,中金公司保荐,费用为9,292.8万元;承销保荐费用最低的是宏海科技,费用仅1,180.54万元。
承销保荐费用率方面,胜科纳米以12%的费用率在27家公司中排名最高;开发科技以4.50%排名垫底。
值得关注的是华安证券保荐的恒鑫生活,该公司IPO募资10.18亿元,承销保荐费用为8408.35万元,费用率为8.26%。
今年一季度,27家IPO公司中有5家公司实际募资额超过10亿元,分别是开发科技、兴福电子、汉朔科技、恒鑫生活、永杰新材,实际募资额分别为11.69亿元,11.68亿元、11.62亿元、10.18亿元、10.14亿元,承销保荐费用分别为5261.51万元、8207.55万元、9292.8万元、8408.35万元、5168.95万元,承销保荐费用率分别为4.50%、7.03%、8%、8.26%、5.1%,由此可见,恒鑫生活在募资额接近的公司中,承销保荐费用率最高,且明显高于开发科技、永杰新材、兴福电子。
华安证券也凭借恒鑫生活这一单IPO项目,获得8408.35万元承销保荐佣金收入,时隔近三年再次有IPO项目上市。不过值得一提的是,华安证券在这单IPO项目过后,储备的IPO项目数量为0(以交易所受理为标准)。
恒鑫生活高保荐费用率背后,公司间接股东中存在被调查的敏感股东。如合肥悦时景朗股权投资合伙企业(有限合伙)、合肥悦时景晖股权投资合伙企业(有限合伙)两个股东的实际控制人都是高新(天眼查数据),而高新曾担任安徽省国际信托投资公司证券发行部副经理、证券营业部经理,安徽国元信托投资有限责任公司总经理助理,国元证券投资银行总部总经理、总裁助理、副总裁,国元证券股份有限副总裁。据悉,高新因违规入股IPO企业而遭受调查,详见《华安证券投行利润连续为负背后:近两年IPO承销收入为0 保荐“独苗”浮现问题股东》等文章。
券商排名情况:“三中”跌出前三 中信建投承销额同比大降56%
今年1-3月份,27家IPO企业合计募资164.76亿元, 19家券商承销这为数不多的金额。
承销额排名前五的券商分别为华泰联合、东兴证券、申万宏源、中信证券、中金公司,承销额分别为22.29亿元、17.94亿元、12.95亿元、11.69亿元、11.62亿元,承销保荐收入分别为1.31亿元、1.16亿元、1.02亿元、1亿元、0.93亿元。

曾经“三中一华”中“三中”,今年一季度IPO承销额排名皆跌出前三。尤其是中信建投,今年一季度以3.47亿元的IPO承销额在19家券商中排名垫底,该承销额较2024年一季度同比大降56%。
当然,也有很多中型投行IPO承销过了一个季度还“未开张”,如民生证券、国金证券、国信证券等。尤其是民生证券,在审的IPO项目仅有6家,加上已经注册的2家合计8家,未来的IPO承销收入虽能温饱,但实现大跨步前进还是有待检验。
下一篇:圣农发展:4月3日召开董事会会议
有话要说...