李斌邀请王传福体验蔚来ET9:感谢传福哥点赞,一起加电
- 每日快讯
- 2025-03-29 18:15:03
- 7
- 更新:2025-03-29 18:15:03
专题:中国电动汽车百人会论坛(2025)
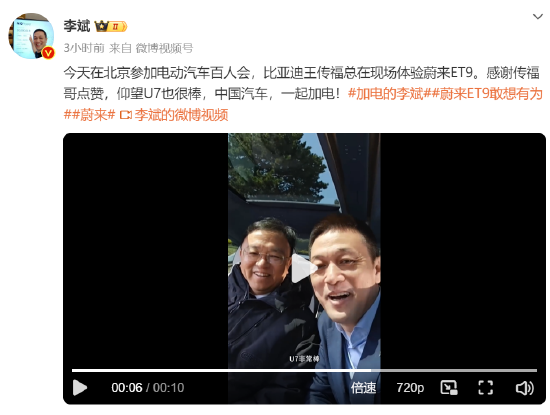
3月29日,在中国电动汽车百人会论坛期间,蔚来创始人李斌邀请比亚迪董事长王传福现场体验蔚来ET9。李斌发布微博称,感谢传福哥点赞,仰望U7也很棒,中国汽车,一起加电!
发布的视频中,李斌问王传福ET9怎么样?王传福附和道:“很不错。”
李斌则接着说:“仰望U7也很棒,我们一起加电。”
新浪声明:所有会议实录均为现场速记整理,未经演讲者审阅,新浪网登载此文出于传递更多信息之目的,并不意味着赞同其观点或证实其描述。